原子性可见性有序性

数据结构与算法

1.线性表

表示n个数据元素的有限序列.元素的数据可以是字母,数字,符号,对象,结构等

线性表包括线性顺序表,线性链表

1.1线性-顺序表

里面元素的内存空间地址是连续的序存储结构，

#####1.2 线性-链表
链式存储结构,里面节点的内存空间地址不是连续的，是通过指针连起来的。

1.2.1 循环链表

链式存储结构,特点最后一个节点的指针指向头节点

1.2.2 双向链表

双向链表的节点中有两个指针,一个指向后,一个指向前

####1.3 栈

1.3.1定义

栈是定义仅在表尾进行插入或删除的线性表

表尾又叫栈顶,表头端叫栈底
特点后进先出

1.3.2栈的表示和实现

1.3.2.1顺序栈

1.3.2.2链栈

1.4 队列

队列是先进先出的线性表
表的一端差入元素,另一端删除元素

1.4.1用链表表示的队列链队列

1.5 树和二叉树

1.5.1 树

树是n个结点的有限集,有且仅有一个特定的根结点
树是一个结点可以有n个结点点 ,每个结点又是一个树,形成一种递归

度
结点拥有的子树的数量称为结点的度

终端结点
度为0的节点称为叶子或总端结点,度不为0的结点称为非终端结点或分支结点,分支结点又称内部结点

数的度是属内各结点的度的最大值

结点的子树根层次结点的还在,该结点称为孩子双亲

结点的层次是从根开始定义起,根为第一层,根的孩子结点为第二层

双亲在同一层的结点互为堂兄,
树中结点的最大层次称为树的深度或高度

1.5.2二叉树

二叉树
二叉树,每个结点最多两棵子树,二叉树的子树有左右之分

满二叉树
一颗深度为k且有2∧k-1个结点的数据称为满二叉树

完全二叉树
对满二叉树的结点进行连续编号,从根结点起,自上而下,从左至右,深度为k的,有n个结点的二叉树,当且仅当每一个结点与满二叉树中的编号从1至n的结点一一对应时,称之为完全二叉树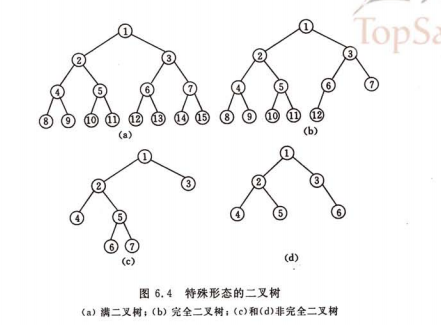
Alt text

性质1
在树的第i层上至多有2∧(i-1)个节点i>=1

性质2
深度为k的二叉树至多有2∧k-1个结点

性质3
度是0的结点数量 = 度是2的结点数量+1

性质4
具有n个结点的完全二叉树的深度为 (log2n)+1

性质5

对任意一个结点i

1.5.3遍历二叉树

先序遍历：
（1）访问根节点；
（2）采用先序递归遍历左子树；
（3）采用先序递归遍历右子树；

中序遍历：
按照左子树->根节点->右子树的顺序访问

后序遍历：
（1）采用后序递归遍历左子树；
（2）采用后序递归遍历右子树；
（3）访问根节点；

平衡二叉搜索树

平衡二叉搜索树（Balanced Binary Tree）具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。常用算法有红黑树、AVL、Treap、伸展树等。在平衡二叉搜索树中，我们可以看到，其高度一般都良好地维持在O（log（n）），大大降低了操作的时间复杂度。

红黑树

红黑树就是一种平衡的二叉查找树，说他平衡的意思是他不会变成“瘸子”，左腿特别长或者右腿特别长。除了符合二叉查找树的特性之外，还具体下列的特性：

1. 节点是红色或者黑色

2. 根节点是黑色

3. 每个叶子的节点都是黑色的空节点（NULL）

4. 每个红色节点的两个子节点都是黑色的。

5. 从任意节点到其每个叶子的所有路径都包含相同的黑色节点。

红黑树相比avl树，在检索的时候效率其实差不多，都是通过平衡来二分查找。但对于插入删除等操作效率提高很多。红黑树不像avl树一样追求绝对的平衡，他允许局部很少的不完全平衡，这样对于效率影响不大，但省去了很多没有必要的调平衡操作，avl树调平衡有时候代价较大，所以效率不如红黑树，在现在很多地方都是底层都是红黑树的天下啦~

红黑树的优势
总结
HashMap在里面就是链表加上红黑树的一种结构，这样利用了链表对内存的使用率以及红黑树的高效检索，是一种很happy的数据结构。